Exploring Satellite Types and Their Orbits: A Journey Through Orbital Mechanics

Related Articles

Software-Defined Satellites and Networks: Ushering in Autonomous Satellites and Swarms

3 days ago

Revolutionizing Space Security: AI-Enabled Satellite Swarms

3 days ago

Satellite Swarms and Formation Flying: Revolutionizing Space Missions

4 days ago

Satellites play a crucial role in modern life, providing essential services such as communication, weather forecasting, navigation, and scientific observation. These advanced pieces of technology orbit Earth in various ways, each tailored to specific missions. Understanding the different types of satellites and their orbits, along with the principles of orbital mechanics, provides insight into how these marvels of engineering operate and contribute to our daily lives.

Types of Satellites

1. Communication Satellites

Communication satellites, or comsats, are used to relay telecommunication signals. They are instrumental in television broadcasting, internet services, and telephone communications. Typically, these satellites are placed in geostationary orbit, allowing them to remain fixed over one point on the Earth’s surface.

For more information on Satellite Communication Systems and technologies, Please visit 

2. Weather Satellites

These satellites monitor Earth’s weather and climate. They are divided into two main categories: geostationary and polar-orbiting. Geostationary weather satellites provide constant observation of a particular area, while polar-orbiting satellites offer global coverage, passing over the poles and gathering data from different regions as the Earth rotates.

3. Navigation Satellites

Navigation satellites, such as those in the GPS constellation, provide positioning, navigation, and timing services. These satellites are typically found in medium Earth orbit (MEO), ensuring a constant and accurate signal for navigation purposes.

4. Earth Observation Satellites

These satellites are designed to monitor and study the Earth’s surface and atmosphere. They are used in environmental monitoring, agriculture, and urban planning. Earth observation satellites often utilize low Earth orbits (LEO) to capture high-resolution images and data.

5. Scientific Satellites

Scientific satellites carry instruments for research purposes, studying everything from Earth’s magnetosphere to the far reaches of space. These can be found in a variety of orbits depending on their specific mission needs.

Understanding Orbits and Orbital Mechanics

Geostationary Orbit (GEO)

A geostationary orbit is a circular orbit approximately 35,786 kilometers above Earth’s equator. Satellites in GEO have an orbital period that matches the Earth’s rotation period (24 hours). This allows the satellite to stay fixed over one point on the Earth’s surface, making it ideal for communication and weather observation purposes.

Geosynchronous Orbit (GSO) & Geostationary Orbit (GEO)

Objects in GSO have an orbital speed that matches the Earth’s rotation, yielding a consistent position over a single longitude. GEO is a kind of GSO. It matches the planet’s rotation, but GEO objects only orbit Earth’s equator, and from the ground perspective, they appear in a fixed position in the sky. GSO and GEO are used for telecommunications and Earth observation. They cannot cover the high latitudes.

Low Earth Orbit (LEO)

LEO is the region of space within 2,000 kilometers of the Earth’s surface. Satellites in LEO orbit the Earth approximately every 90 minutes. This orbit is favored for Earth observation and some communication satellites due to the proximity to Earth, allowing for high-resolution imaging and low-latency communication.

Medium Earth Orbit (MEO)

MEO lies between LEO and GEO, typically ranging from 2,000 to 35,786 kilometers above the Earth. Navigation satellites, like those in the GPS system, are commonly found in MEO. This orbit provides a balance between coverage area and signal delay, making it suitable for navigation.

Highly Elliptical Orbit (HEO) Satellites:

Venturing further out, HEO satellites travel in elliptical paths, allowing them to spend extended periods over specific regions. They’re used for applications like military surveillance and deep space exploration.

Polar Orbit

Polar orbits pass over the Earth’s poles, allowing satellites to scan the entire surface of the Earth over time. These orbits are often used by weather and Earth observation satellites. A polar orbit’s altitude can vary, but it often lies within LEO. They fly several hundred km over the earth’s surface with a rotation period of about 110 minutes. They can cover most of the earth’s surface except for regions immediately adjacent to the poles. They have an inclination that measures the angle at which they cross the equator and which determines how close they get to passing directly over the poles.

Sun-Synchronous Orbit

A special type of polar orbit, the sun-synchronous orbit, ensures that the satellite passes over the same part of the Earth at the same local solar time. This consistency in lighting conditions is essential for imaging satellites used in Earth observation and environmental monitoring.

Molniya orbits are highly eccentric Earth orbits with periods of approximately 12 hours (2 revolutions per day). The orbital inclination is chosen so the rate of change of perigee is zero, thus both apogee and perigee can be maintained over fixed latitudes. This condition occurs at inclinations of 63.4 degrees and 116.6 degrees. For these orbits the argument of perigee is typically placed in the southern hemisphere, so the satellite remains above the northern hemisphere near apogee for approximately 11 hours per orbit. This orientation can provide good ground coverage at high northern latitudes.

Hohmann transfer orbits are interplanetary trajectories whose advantage is that they consume the least possible amount of propellant. A Hohmann transfer orbit to an outer planet, such as Mars, is achieved by launching a spacecraft and accelerating it in the direction of Earth’s revolution around the sun until it breaks free of the Earth’s gravity and reaches a velocity which places it in a sun orbit with an aphelion equal to the orbit of the outer planet. Upon reaching its destination, the spacecraft must decelerate so that the planet’s gravity can capture it into a planetary orbit.

Orbital Mechanics

Orbital mechanics is the study of the motions of artificial satellites and space vehicles under the influence of forces such as gravity. Orbital mechanics, also known as astrodynamics, is the branch of aerospace engineering that deals with the motion of spacecraft. It applies principles from ballistics and celestial mechanics to address the practical problems concerning the trajectories and behaviors of rockets and satellites. The movement of these objects is governed primarily by Newton’s laws of motion and the law of universal gravitation. Orbital mechanics is a fundamental discipline in space-mission design and control, ensuring that satellites and other spacecraft achieve and maintain their intended orbits.

Key principles include:

Kepler’s Laws of Planetary Motion

Kepler’s laws describe the motion of planets around the sun and are equally applicable to satellites orbiting Earth. These laws are:

1. Law of Orbits: Planets move in elliptical orbits with the sun at one focus. For satellites, this means they orbit Earth in ellipses with Earth at one focus. A circle is a special case of an ellipse where both foci coincide at the center.

   

   An ellipse is defined to be a curve with the following property: for each point on an ellipse, the sum of its distances from two fixed points, called foci, is constant. The longest and shortest lines that can be drawn through the center of an ellipse are called the major axis and minor axis, respectively. The semi-major axis is one-half of the major axis and represents a satellite’s mean distance from its primary. Eccentricity is the distance between the foci divided by the length of the major axis and is a number between zero and one. An eccentricity of zero indicates a circle.

2. Law of Areas: A line segment joining a planet and the sun sweeps out equal areas during equal intervals of time. Similarly, a satellite’s orbital path covers equal areas in equal times, meaning its speed varies depending on its distance from Earth.
3. Law of Periods: The square of a satellite’s orbital period is proportional to the cube of the semi-major axis of its orbit. This relationship allows for the calculation of the satellite’s speed based on its average distance from Earth.

• The square of a satellite’s orbital period is proportional to the cube of its average distance from the planet. Kepler’s third law of orbital motion gives us a precise relationship between the speed of the satellite and its distance from the earth.  An Earth-orbiting satellite’s motion is mostly controlled by Earth’s gravity. As satellites get closer to Earth, the pull of gravity gets stronger, and the satellite moves more quickly.

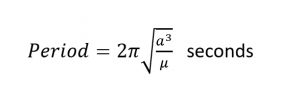
a is the semi-major axis, which describes the size of the orbit and  is called the gravitational constant   G is the universal gravitational constant and M is the mass of the central body.  This unsurprisingly means that the larger the orbit,  the longer it takes for the object to traverse it   For Earth, this gravitational constant is approximately 398,600.5 km³/s².

Newton’s Law of Universal Gravitation

This law states that every point mass attracts every other point mass in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This fundamental principle governs the motion of satellites in orbit.

Forces at Play: Maintaining the Orbital Balance

Two primary forces keep satellites in their designated orbits:

• Gravity: Earth’s gravity pulls the satellite inwards, constantly trying to bring it closer.
• Centrifugal Force: The satellite’s inertia, due to its high speed, pushes it outwards, trying to fling it away from Earth.

In a stable orbit, these forces perfectly balance each other. If the satellite loses too much speed (due to air drag or other factors), gravity can overpower it, causing it to re-enter the atmosphere and burn up. Conversely, if it gains too much speed (due to a propulsion boost), the centrifugal force can overpower gravity, sending it into a higher orbit or even escaping Earth’s influence altogether.

Orbital Elements

To describe an orbit mathematically, six quantities known as orbital elements are used:

• Epoch: The specific time at which the orbital elements are defined. A set of orbital elements is a snapshot, at a particular time, of the orbit of a satellite. Epoch is simply a number that specifies the time at which the snapshot was taken.
• Orbital Inclination: The tilt of the satellite’s orbit plane relative to Earth’s equatorial plane, measured in degrees. The orbit ellipse lies in a plane known as the orbital plane. The orbital plane always goes through the center of the earth, but may be tilted any angle relative to the equator. Inclination is the angle between the orbital plane and the equatorial plane. By convention, inclination is a number between 0 and 180 degrees.Orbits with inclination near 0 degrees are called equatorial orbits (because the satellite stays nearly over the equator). Orbits with inclination near 90 degrees are called polar (because the satellite crosses over the north and south poles). The intersection of the equatorial plane and the orbital plane is a line which is called the line of nodes.
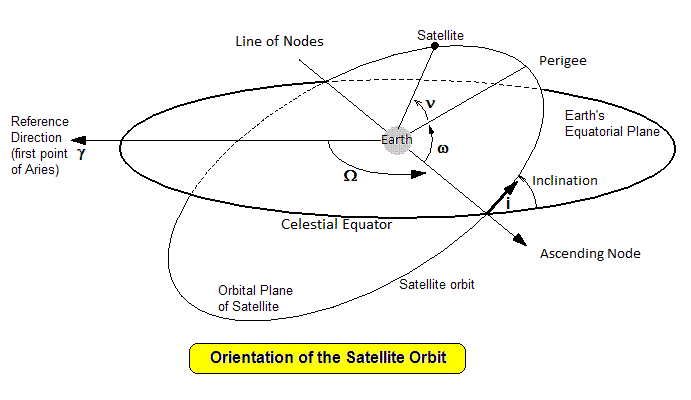
• Right Ascension of Ascending Node (RAAN): The angle from the vernal equinox to the point where the satellite crosses the equatorial plane from south to north. Two numbers orient the orbital plane in space. The first number was Inclination. “right ascension of ascending node” is an angle, measured at the center of the earth, from the vernal equinox to the ascending node. The intersection of the equatorial plane and the orbital plane is a line which is called the line of nodes.  One of two nodes is called the ascending node (where the satellite crosses the equator going from south to north). The other is called the descending node (where the satellite crosses the equator going from north to south). By convention, we specify the location of the ascending node. By convention, RAAN is a number in the range 0 to 360 degrees. Vernal equinox is nothing more than the ascending node of the Sun’s orbit. The Sun’s orbit has RAAN = 0 simply because we’ve defined the Sun’s ascending node as the place from which all ascending nodes are measured. The RAAN of your satellite’s orbit is just the angle (measured at the center of the earth) between the place the Sun’s orbit pops up past the equator, and the place your satellite’s orbit pops up past the equator.
• Argument of Perigee: The angle between the ascending node and the orbit’s point of closest approach to Earth (perigee). Now that we’ve oriented the orbital plane in space, we need to orient the orbit ellipse in the orbital plane. We do this by specifying a single angle known as argument of perigee. The line-of-apsides passes through the center of the earth. We’ve already identified another line passing through the center of the earth: the line of nodes. The angle between these two lines is called the argument of perigee. Where any two lines intersect, they form two supplementary angles, so to be specific, we say that argument of perigee is the angle (measured at the center of the earth) from the ascending node to perigee.
• Eccentricity: A measure of the orbit’s deviation from a perfect circle (ranging from 0 for a circle to near 1 for a highly elongated ellipse). In the Keplerian orbit model, the satellite orbit is an ellipse. Eccentricity tells us the “shape” of the ellipse. When e=0, the ellipse is a circle. When e is very near 1, the ellipse is very long and skinny.
• Mean Anomaly: The fraction of the orbital period that has elapsed since the satellite passed the perigee, expressed as an angle. Mean Motion: Kepler’s third law of orbital motion gives us a precise relationship between the speed of the satellite and its distance from the earth. Satellites that are close to the earth orbit very quickly. Satellites far away orbit slowly. This means that we could accomplish the same thing by specifying either the speed at which the satellite is moving or its distance from the earth. Satellites in circular orbits travel at a constant speed.  We just specify that speed, and we’re done. Satellites in non-circular (i.e., eccentricity > 0) orbits move faster when they are closer to the earth, and slower when they are farther away. The common practice is to average the speed. You could call this number “average speed”, but astronomers call it the “Mean Motion”. Mean Motion is usually given in units of revolutions per day. Sometimes “orbit period” is specified as an orbital element instead of Mean Motion. The period is simply the reciprocal of Mean Motion. A satellite with a Mean Motion of 2 revs per day, for example, has a period of 12 hours.
• Now that we have the size, shape, and orientation of the orbit firmly established, the only thing left to do is specify where exactly the satellite is on this orbit ellipse at some particular time. Our very first orbital element (Epoch) specified a particular time, so all we need to do now is specify where, on the ellipse, our satellite was exactly at the Epoch time. Anomaly is yet another astronomer word for angle. Mean anomaly is simply an angle that marches uniformly in time from 0 to 360 degrees during one revolution. It is defined to be 0 degrees at perigee, and therefore is 180 degrees at apogee.
• Drag (optional):Drag caused by the earth’s atmosphere causes satellites to spiral downward. As they spiral downward, they speed up. The Drag orbital element simply tells us the rate at which Mean Motion is changing due to drag or other related effects. Precisely, Drag is one half the first time derivative of Mean Motion. Its units are revolutions per day per day. It is typically a very small number. Common values for low-earth-orbiting satellites are on the order of 10^-4. Common values for high-orbiting satellites are on the order of 10^-7 or smaller.

The real world is slightly more complex than the Keplerian model, and tracking programs compensate for this by introducing minor corrections to the Keplerian model. These corrections are known as perturbations.

Orbital Maneuvers

Orbital Maneuvers

Satellites can change their orbits through orbital maneuvers, typically involving the use of onboard thrusters. To change a satellite’s orbit, propulsion systems are used to perform maneuvers such as Hohmann transfers (for moving between two orbits) or inclination changes (to alter the orbital plane). These maneuvers require precise calculations to ensure successful transitions.

Common maneuvers include:

1. Hohmann Transfer Orbit:

• A fuel-efficient method to transfer between two orbits by applying thrust at two specific points (periapsis and apoapsis).

2. Bi-elliptic Transfer:

• A two-step maneuver used to transfer between orbits with a large difference in altitude, often more efficient than a Hohmann transfer for very high orbits.

3. Plane Change Maneuver:

• Alters the inclination of the orbit, often combined with altitude changes to optimize fuel use.

Without applying force (such as firing a rocket engine), the period and shape of the satellite’s orbit won’t change. If thrust is applied at only one point in the satellite’s orbit, it will return to that same point on each subsequent orbit, though the rest of its path will change. Thus one cannot move from one circular orbit to another with only one brief application of thrust.

From a circular orbit, thrust applied in a direction opposite to the satellite’s motion changes orbit to elliptical; the satellite will descend and reach the lowest orbital point (the periapse) at 180 degrees away from the firing point; then it will ascend back. Thrust applied in the direction of the satellite’s motion creates an elliptical orbit with its highest point (apoapse) 180 degrees away from the firing point.

Conclusion

Satellites and their orbits are marvels of modern engineering and science, each tailored to meet specific needs and challenges. From communication and navigation to weather monitoring and scientific research, satellites serve as indispensable tools. Understanding the types of satellites, their orbits, and the principles of orbital mechanics provides a deeper appreciation for the technological achievements that keep our world connected and informed. As technology advances, we can expect even more sophisticated satellites and innovative orbital strategies to emerge, further expanding our capabilities in space.

 

 

 

 

 

References and resources also include:

https://www.amsat.org/keplerian-elements-tutorial/