As satellite constellations become integral to global communication networks, ensuring reliable and efficient data transmission remains a paramount challenge. Channel coding, which adds redundancy to transmitted data, is a fundamental technique employed to enhance the reliability and efficiency of satellite communication systems. This article delves into the principles of channel coding, its application in satellite constellations, and its critical role in maintaining robust communication.
The rise of mega-constellations promises ubiquitous internet access and expanded mobile connectivity. But venturing into the vast expanse brings unique challenges. Unlike terrestrial networks, mobile satellite communications contend with harsh channel effects like:
- Path Loss: The sheer distance between satellites and Earth-bound users weakens the signal.
- Doppler Shift: Satellite movement induces frequency variations, distorting the signal.
- Multipath Fading: The signal can bounce off various objects, creating distorted replicas that interfere with the original transmission.
These effects elevate the Bit Error Rate (BER), meaning more errors creep into the data stream. Here’s where channel coding comes in as a hero, playing a vital role in ensuring reliable data transmission for mobile satellite constellations.
The Principle of Channel Encoding
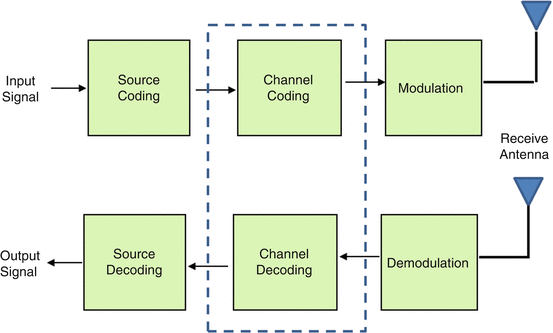
Channel encoding involves adding redundant bits to the information bits to form a coded sequence, which is then transmitted over the channel. The primary objective of this process is to enable error detection and correction at the receiver. This technique, known as forward error correction (FEC), enhances the reliability of data transmission in the presence of noise and other impairments.
Code Rate
The code rate (r) is a key parameter in channel coding and is defined as the ratio of information bits (n) to the total number of bits (n + r), where r represents the number of redundant bits. Mathematically, the code rate is expressed as:
The equation for code rate (r) remains the same as provided in the passage:
code rate r = n / (n + k)
Here:
- k: Number of redundant bits added for n information bits.
- n: Number of information bits.
2. Bit Rate at Encoder Output:
The equation for bit rate at the encoder output (Rc) is modified to account for the code rate:
Rc = Rb / r (bit/s)
Here:
- Rc: Bit rate at the encoder output (including redundant bits).
- Rb: Bit rate at the encoder input (information bits only).
- r = Code rate .
Decoding Gain and Eb/N0 Relationship:
The equation for Eb/N0 considering code rate is already provided in the passage:
Eb/N0 = Ec/N0 – 10 log r (dB)
Here:
- Eb/N0: Energy per information bit to noise power spectral density ratio (dB).
- Ec/N0: Energy per coded bit to noise power spectral density ratio (dB).
- r: Code rate
The decoding gain Gcod is defined as the difference in decibels (dB) at the considered value of bit error probability (BEP) between the
required values of Eb=N0 with and without coding, assuming equal information bit rate Rb.
These equations, along with the understanding of code rate, provide a foundation for analyzing and optimizing channel coding performance in satellite communication systems.
Encoding Techniques
Two primary encoding techniques are used in mobile satellite networks: block encoding and convolutional encoding.
Block Encoding
In block encoding, the encoder associates redundant bits with each block of information bits. Each block is coded independently, and the code bits are generated through a linear combination of the information bits within the block. Cyclic codes, particularly Reed-Solomon (RS) and Bose, Chaudhari, and Hocquenghem (BCH) codes, are commonly used in block encoding due to their robustness in correcting burst errors.
Convolutional Encoding
Convolutional encoding generates a sequence of coded bits from a continuous stream of information bits, taking into account the current and previous bits. This technique is characterized by its use of shift registers and exclusive OR adders, which determine the encoded output based on a predefined constraint length.
The choice between block and convolutional encoding depends on the expected error patterns at the demodulator output. Convolutional encoding is effective under stable propagation conditions and Gaussian noise, where errors occur randomly. Conversely, block encoding is preferred in fading conditions where errors occur in bursts.
Channel Decoding
Forward error correction (FEC) at the decoder involves utilizing the redundancy introduced during encoding to detect and correct errors. Various decoding methods are available for block and convolutional codes.
Decoding Block Cyclic Codes
For block cyclic codes, a common decoding method involves calculating and processing syndromes, which result from dividing the received block by the generating polynomial. If the transmission is error-free, the syndrome is zero.
Decoding Convolutional Codes: The Viterbi Algorithm
Convolutional codes are a type of error-correcting code used in digital communications to improve the reliability of data transmission over noisy channels. Decoding these codes involves determining the most likely sequence of transmitted data bits given the received noisy signal. The Viterbi algorithm is the most widely used method for decoding convolutional codes, providing optimal performance in terms of error correction.
Understanding Convolutional Codes
In a convolutional coding system:
- Input Data Stream (u): A stream of data bits to be transmitted.
- Encoded Output (v): A stream of encoded bits, where each set of input bits is transformed into a set of output bits using a convolutional encoder. The relationship between input and output bits is determined by the code rate (R_c), which is the ratio of input bits to output bits (e.g., R_c = 1/2 means each input bit is transformed into two output bits).
The convolutional encoder introduces redundancy, allowing the decoder to detect and correct errors that occur during transmission.
The Viterbi Algorithm for Decoding
The Viterbi algorithm is a maximum likelihood decoding algorithm that operates by finding the most likely sequence of encoded bits that could have generated the received noisy signal. It does so by examining all possible paths through a trellis diagram, which represents the state transitions of the convolutional encoder.
- Trellis Diagram: The trellis diagram is a graphical representation of the state transitions of the convolutional encoder. Each state represents a possible memory configuration of the encoder, and transitions between states correspond to the encoding of input bits.
- Path Metric: The Viterbi algorithm calculates a path metric for each possible path through the trellis, which is a measure of how closely the received signal matches the expected signal for that path. The path with the lowest metric (least errors) is chosen as the most likely transmitted sequence.
- Survivor Path: At each step, the algorithm retains only the most likely path (survivor path) leading to each state. This significantly reduces the complexity of the decoding process by eliminating less likely paths.
Bit Error Probability (BEP)
- Before Decoding (BEP_in): The bit error probability at the decoder input (BEP_in) reflects the likelihood that a bit received over the noisy channel is incorrect. This is influenced by the channel conditions and the noise level.
- After Decoding (BEP_out): After the Viterbi algorithm has decoded the received signal, the bit error probability at the output (BEP_out) is significantly reduced. This reduction occurs because the algorithm corrects many of the errors introduced during transmission by selecting the most likely transmitted sequence.
Key Steps in the Viterbi Decoding Process
- Initialization: Set the initial path metric for the starting state (usually the all-zeros state) to zero, and all other states to infinity.
- Recursion: For each received symbol, update the path metrics for all possible states in the trellis by considering the metrics of paths leading to those states. Retain only the most likely path to each state.
- Termination: Once all received symbols have been processed, trace back through the trellis along the survivor path to reconstruct the most likely transmitted sequence.
- Output: The output sequence is the decoded data, with errors corrected based on the maximum likelihood path.
Benefits of the Viterbi Algorithm
- Optimal Error Correction: The Viterbi algorithm provides optimal decoding in terms of minimizing the bit error rate, making it highly effective for communication systems requiring reliable data transmission.
- Widely Used: It is widely used in various communication standards, including satellite communications, mobile networks, and wireless LANs, due to its effectiveness and feasibility of implementation.
- Reduced BEP: The algorithm’s ability to correct errors results in a significant reduction in the bit error probability (BEP_out) compared to the input BEP, improving the overall reliability of the communication system.
In summary, the Viterbi algorithm plays a crucial role in decoding convolutional codes, enabling reliable communication over noisy channels by effectively reducing the bit error rate through optimal error correction.
Energy per Bit
The bit error probability is typically expressed as a function of Eb/N0, where Eb represents the energy per information bit; that is, the amount of power accumulated from the carrier over the duration of the considered information bit. As the carrier power is C, and the duration of the information bit is Tb = 1/ Rb, where Rb is the information bit rate, then Eb is equal to C/Rb. This relationship is crucial in determining the required signal power for a given error rate. The decoding gain Gcod is defined as the difference in decibels (dB) between the required values of EbN0 with and without coding for the same bit error probability.
Concatenated Encoding
To further enhance error correction capabilities, block encoding and convolutional encoding can be combined in a concatenated encoding scheme. This approach involves an outer block encoder followed by an inner convolutional encoder. At the receiver, the inner decoder first corrects errors, and the outer decoder subsequently corrects any residual errors.
The outer decoder is able to correct the occasional bursts of errors generated by the inner decoder’s decoding algorithm, which produces such bursts of errors whenever the number of errors in the incoming bit stream oversteps the correcting capability of the algorithm. The performance of concatenated encoding is improved while using simple outer coders by implementing interleaving and deinterleaving between the outer and inner coders.
Concatenated encoding is employed in standards such as DVB-S and DVB-S2. For instance, DVB-S uses an RS (204, 188) outer block encoder and a convolutional inner encoder with varying code rates. DVB-S2 enhances this by incorporating BCH and LDPC codes for the outer and inner encoding stages, respectively, achieving performance close to the Shannon limit.
Combining Modulation and Error Correction: Coded Modulation
Coded modulation is a technique used in digital communications that combines two important processes: modulation and error correction coding. Let’s break down these concepts in simpler terms.
Modulation and Error Correction Coding
- Modulation: This is the process of converting digital information (bits) into a signal that can be transmitted over a communication channel, such as a satellite link. Different modulation schemes (like QPSK, 8-PSK, and 16-QAM) represent data using different patterns of signal changes.
- Error Correction Coding (ECC): This adds extra bits to the original data to help detect and correct errors that might occur during transmission. These extra bits increase the overall bit rate, meaning more bandwidth is needed.
Traditionally, these two processes are done separately. However, this separate approach can lead to inefficiencies, especially when dealing with high data rates and limited bandwidth.
Coded modulation integrates modulation and error correction into a single process. Here’s how it works:
- Integrated Approach: Instead of adding redundant bits separately, coded modulation expands the set of signal patterns (called the alphabet) used in modulation.
- Larger Alphabet: For example, instead of using a simple 4-symbol set (like in QPSK), coded modulation might use an 8-symbol set (like in 8-PSK) or even larger. This means more bits can be transmitted in each symbol duration.
- Efficient Use of Bandwidth: By using a larger set of symbols, coded modulation can transmit more information without significantly increasing the required bandwidth.
Benefits of Coded Modulation
- Improved Error Performance: Coded modulation reduces the energy per bit needed to achieve a certain error rate. For example, coded 8-PSK can perform significantly better (up to 6 dB gain) than uncoded QPSK for the same spectral efficiency.
- Spectral Efficiency: Although coded modulation may have slightly less spectral efficiency than the pure higher-order modulations (like 16-QAM), it achieves better overall performance in terms of error rates.
Key Concepts in Coded Modulation
- Symbol Duration (Ts): The time period during which each symbol is transmitted.
- Free Distance (dfree): A measure of the minimum distance between sequences of symbols in the coded modulation scheme. A larger dfree means lower error probability.
- Asymptotic Coding Gain (Gcod(∞)): The improvement in error performance as the signal-to-noise ratio becomes very high. It’s a measure of how much better the coded modulation performs compared to uncoded modulation.
Types of Coded Modulation
- Trellis Coded Modulation (TCM): Uses convolutional encoding, which means the encoded output depends on the current and previous input bits, forming a “trellis” structure.
- Block Coded Modulation (BCM): Uses block encoding, where data is encoded in fixed-size blocks.
Trellis-Coded Modulation (TCM) for 8-PSK
Trellis-Coded Modulation (TCM) is an advanced technique that combines modulation and coding to enhance the error performance of communication systems, particularly over noisy channels such as satellite links. When using an 8-PSK (8-Phase Shift Keying) scheme, each symbol represents 3 bits of data, enabling efficient use of bandwidth. The goal of TCM is to maximize the minimum distance between possible transmitted signals thereby reducing the probability of errors.
Set partitioning is a key step in TCM where the set of 8-PSK symbols is divided into smaller subsets. This partitioning is done in a way that maximizes the distance between points within each subset, which is crucial for minimizing errors. Each subset is associated with different paths in the trellis diagram. The partitioning is done hierarchically in multiple levels, with each level representing a finer subdivision of the symbol set, ultimately leading to a structure that facilitates effective error correction.
A trellis diagram visually represents the state transitions of the TCM encoder over time. Each state in the trellis corresponds to a specific condition of the encoder’s memory elements. The diagram helps in understanding how the encoder processes input bits and maps them to output symbols while maintaining a memory of past states, which is essential for the coding process.
The theoretical maximum spectral efficiency of 8-PSK is 3 bits/s/Hz. However, with TCM, the effective spectral efficiency is 2 bits/s/Hz due to the inclusion of coding. Despite this, the TCM scheme offers significant power savings by providing a coding gain. This gain is achieved by requiring less transmitted power to maintain the same level of error performance as compared to an uncoded scheme.
The typical configuration of a TCM encoder involves encoding some of the input bits using a binary convolutional encoder, while other bits are left uncoded. This hybrid approach balances error protection and complexity. The encoded bits provide robust error correction, while the uncoded bits allow for efficient use of bandwidth. This structure ensures that the most critical bits are better protected against errors, enhancing the overall reliability of the communication system.
In summary, TCM using 8-PSK modulation improves the reliability and efficiency of data transmission over satellite channels by integrating modulation and coding. The set partitioning, trellis diagram, and strategic encoding provide robust error correction while maintaining high spectral efficiency, making TCM a powerful technique for communication systems.
Optimizing for Constellation Dynamics
The choice of coding scheme depends on various factors specific to the constellation design:
- Orbital Altitude: Low Earth Orbit (LEO) constellations experience rapid Doppler shifts, favoring convolutional codes. Geostationary Earth Orbit (GEO) constellations have less severe Doppler effects, making turbo codes a viable option.
- Data Rates: Higher data rates demand more complex coding schemes for robust error correction. However, these come at the expense of increased decoding complexity, a constraint for mobile user terminals with limited processing power.
Satellite constellations, comprising multiple satellites in low Earth orbit (LEO), medium Earth orbit (MEO), or geostationary orbit (GEO), demand robust and efficient channel coding techniques to maintain reliable communication links.
Low Earth Orbit (LEO) Satellites
LEO satellites, due to their lower altitude, experience rapid changes in propagation conditions and frequent handovers between satellites. Channel coding in LEO constellations must be capable of handling burst errors and varying signal quality. Concatenated encoding schemes, particularly those combining RS and convolutional codes, are well-suited for these conditions.
Medium Earth Orbit (MEO) Satellites
MEO satellites operate at higher altitudes than LEO satellites, offering longer communication windows and more stable propagation conditions. However, they still encounter significant signal degradation due to distance and atmospheric effects. Block encoding techniques, such as RS and BCH codes, provide robust error correction capabilities for MEO satellite communication.
Geostationary Orbit (GEO) Satellites
GEO satellites maintain a fixed position relative to the Earth’s surface, providing consistent and stable communication links. The primary challenge for GEO satellites is mitigating the impact of Gaussian noise and occasional signal fading. Convolutional encoding, coupled with advanced decoding algorithms like the Viterbi algorithm, is highly effective in this scenario.
Emerging Techniques
The field of channel coding is constantly evolving. Here are some promising techniques for future mobile satellite constellations:
1. Low-Density Parity-Check (LDPC) Codes:
- Concept: Unlike traditional error correcting codes with dense parity-check matrices (lots of 1s), LDPC codes use sparse matrices with a low density of 1s. This sparsity allows for efficient decoding algorithms.
- Decoding Power: LDPC codes achieve near-capacity performance, meaning they can correct errors up to the theoretical limit imposed by channel noise.
- Decoding Algorithms: Iterative decoding algorithms like belief propagation are used. These algorithms work by passing messages between variable nodes (data bits) and check nodes (parity checks) in the LDPC code’s graphical representation (Tanner graph). With each iteration, the messages get refined, leading to improved error correction.
2. Iterative Decoding:
- Traditional vs. Iterative: Traditional decoding approaches often involve a single decoding pass. Iterative decoding, on the other hand, performs multiple decoding passes, progressively improving the decoded data.
- Combining Multiple Codes: This technique allows for the joint decoding of multiple codes applied to the data. For example, an LDPC code could be combined with a convolutional code.
- Improved Performance: By iteratively decoding these combined codes, the decoder can leverage the strengths of each code, potentially achieving superior error correction compared to single-code decoding.
3. Network Coding:
- Beyond Traditional Coding: Network coding breaks away from the paradigm of transmitting data packets unchanged. Instead, it strategically combines information packets at different network nodes.
- Exploiting Network Topology: Network coding utilizes the network’s structure to create redundant information at various nodes. This redundancy can then be used to reconstruct lost data packets even if some transmissions are corrupted.
- Enhanced Reliability: In mobile satellite networks, where channel effects can be severe, network coding offers a way to improve overall network reliability by creating multiple paths for data to reach its destination.
These emerging techniques offer exciting possibilities for future mobile satellite constellations. LDPC codes with their efficient decoding and near-capacity performance, iterative decoding for potentially superior error correction, and network coding for enhanced reliability through network-aware data manipulation, all hold promise in creating robust and efficient communication systems.
Recent Breakthroughs
While the core concepts of LDPC codes, iterative decoding, and network coding remain at the forefront of satellite channel coding, recent breakthroughs are pushing the boundaries of performance and efficiency:
1. Tailored Code Construction for Specific Channel Conditions:
- Traditionally, “one-size-fits-all” coding schemes were used. Recent research focuses on constructing LDPC codes specifically tailored to the expected channel conditions for a particular satellite constellation.
- This can involve optimizing the code’s parity-check matrix structure based on factors like Doppler shift and path loss. By customizing the code to the channel, researchers are achieving even better error correction performance.
2. Faster Decoding Algorithms with Hardware Acceleration:
- LDPC code decoding, while powerful, can be computationally intensive for high data rates. Recent breakthroughs involve developing faster decoding algorithms with hardware acceleration.
- This can involve utilizing specialized hardware like Field-Programmable Gate Arrays (FPGAs) or Application-Specific Integrated Circuits (ASICs) optimized for LDPC decoding. This hardware acceleration allows for real-time processing of high-bandwidth data streams from satellites.
3. Integration with Modulation and Forward Error Correction (FEC) Schemes:
- Channel coding often works in conjunction with modulation techniques and Forward Error Correction (FEC) schemes. Recent research explores jointly optimizing channel coding, modulation, and FEC for satellite communication.
- By considering these elements as a unified system, researchers are achieving significant improvements in overall communication efficiency and reliability. This co-design approach can unlock new possibilities for maximizing data throughput while minimizing errors.
4. Machine Learning-assisted Decoding for Dynamic Channel Adaptation:
- Satellite channel conditions can be dynamic, and static coding schemes might not always be optimal. Recent advancements involve exploring machine learning (ML) techniques for adaptive decoding.
- In this approach, an ML model analyzes real-time channel information and adjusts the decoding process accordingly. This allows for dynamic adaptation to changing channel conditions, further enhancing the robustness of communication.
These breakthroughs showcase the continuous evolution of satellite channel coding. By tailoring codes, accelerating decoding, and integrating with other communication elements using cutting-edge techniques, researchers are paving the way for a future of high-performance and reliable satellite communication.
Conclusion
Channel coding is indispensable in satellite constellations, providing the necessary error correction capabilities to ensure reliable communication. By incorporating advanced encoding techniques such as block and convolutional encoding, along with concatenated encoding schemes, satellite systems can achieve robust performance even in challenging environments.
These emerging techniques offer exciting possibilities for future mobile satellite constellations. LDPC codes with their efficient decoding and near-capacity performance, iterative decoding for potentially superior error correction, and network coding for enhanced reliability through network-aware data manipulation, all hold promise in creating robust and efficient communication systems. By tailoring codes, accelerating decoding, and integrating with other communication elements using cutting-edge techniques, researchers are paving the way for a future of high-performance and reliable satellite communication.
As satellite technology continues to advance, the principles and applications of channel coding will remain central to the development of efficient and resilient communication systems.
 International Defense Security & Technology Your trusted Source for News, Research and Analysis
International Defense Security & Technology Your trusted Source for News, Research and Analysis